Packed Distillation
Introduction
Packed distillation systems are very common in industry. Their structure is similar to a plate column (e.g. both have an enriching section, stripping section) with the main difference being that instead of plates making up our stages, we have a height of packing. To design a packed distillation column, we essentially draw a preliminary design for a plate column. We use the plate distillation design, and then design the for height of packing needed for our design.
In our previous distillation discussion, we showed that we can theoretically derive many parameters in our system. For example, using the McCabe-Thiele method, we can find the number of theoretical stages a distillation column will need to meet our design specifications. Now those concepts fit quite nicely to a plate distillation column (e.g. each stage is just a plate in a plate column), but plate distillation columns can be expensive and are generally used for high yield systems. In this discussion, we will extend our previous discussion to look at how we can design our packed column. We will finish this discussion by finally looking and comparing plate distillation column and a packed distillation column.
Height Equivalence
The main parameter we need to know in our distillation column is the amount of packing needed. An empirically derived value known as the “Height Equivalent to Theoretical Stage (HETS)” will prove to be useful. This value can convert the number of stages a column needs to a practical height value. In other words, if we use the McCabe-Thiele method, we can determine the number of stages needed for our design. The equation is stated below:
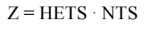
Equation 1, where Z = Packing height
NTS = number of stages
The issue with this methodology is the lack of any theoretical basis behind the derivation of the HETS value. Therefore, this value is not regularly available all the time, and will not take into account factors such wear and tear, impurties, etc. This value is useful when it comes to buying a new distillation column from a recognized vendor.
Say, instead we had to rate a column? In other words, we are being asked to determine how effective the already existent column is or rate some theoretical design? How can we derive this height from first principles?
NTU Derivation of Packing Height
It is possible to derive a differential equation that describes how the concentration of the solutes changes as we go up the column. Since we are able to analyze the concentrations of the feed, distillate and bottom streams, we can set these values as our boundary conditions and use them to solve our differential equation. The actual derivation of this equation is outside of the scope of this course (but you will learn how to derive this equation in CHE311). Thus, we will simply continue our discussion on actually applying the theory for design. The equation comes out to be:
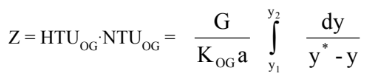
Equation 2 where G = superficial gas velocity, K = mass diffusivity coefficient, and a = porosity
You may have noticed that this equation has a variable we haven’t discussed up until now (y), which is know as the interphase concentration. In a packed column, liquid flowing down the column and gas moving up the column. When these two fluids interact, they create an interphase where the bulk of mass transfer occurs. The average concentration in this phase is held by the y* variable. This value cannot be easily measured or calculated, so how do we use this equation to determine the packing height.
Applying the NTU Equation
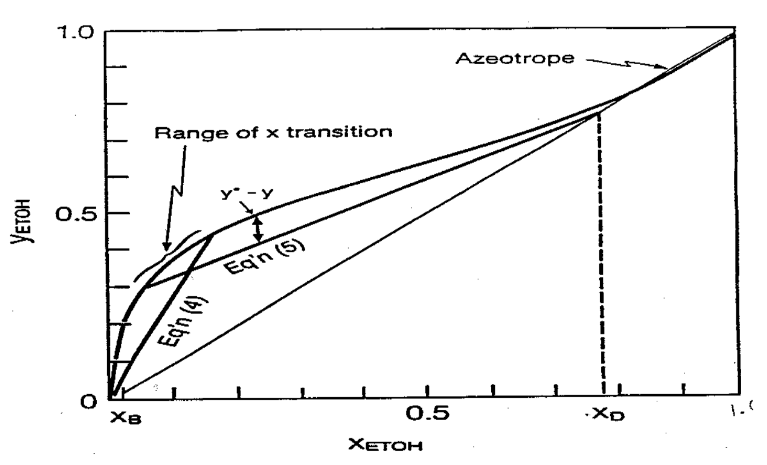
We first begin by drawing the operating lines for the enriching and stripping section. The two lines will intersect and will create an envelope around a certain region on the xy-line. This region essentially gives us the range of interphase, transition concentrations in our column. Scientists have developed empirical equations to determine the interphase concentration. I adapted an equation from Hala et al (1968, p. 192):
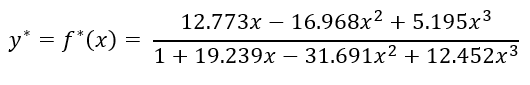
To continue with our analysis, we can rewrite these two operating lines into a different form. Although the equation may look different, it is equivalent to the form we introduced before. Looking back at equation 2, we can set the NTU variable equal to the integral. Do you remember the assumptions we made? We assumed that the volumetric flow of both phases are constant throughout the whole column. In doing so, we can then determine the the speed of each phase in the column is constant. Because of this, we know that the height transfer unit variable (HTU) is constant for both phases throughout the whole column.
Since we are feeding the column halfway through the column, we also know then that the number of transfer units (NTU) is therefore equal in both the enriching and stripping section. Subbing in all our variables into equation to, mathematically the equation comes out to be:
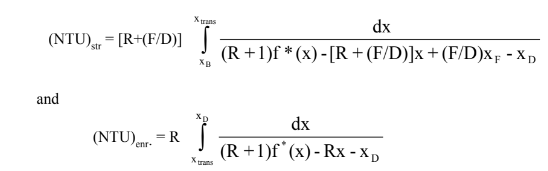
Where R = reflux ratio, F = feed flow rate, D = distillate flow rate
Knowing that these two integrals are equal, we can then use root-finding methods to determine an interphase, transition concentration – which in range of the values found on the graph, so do not accept any solution unless it is within that range – which gives a solution that these two NTU values are equal.
Once you have found the correct NTU, you are then able to multiply this value with the HTU and find the height of the packing needed
Plate Column vs. Packed Column