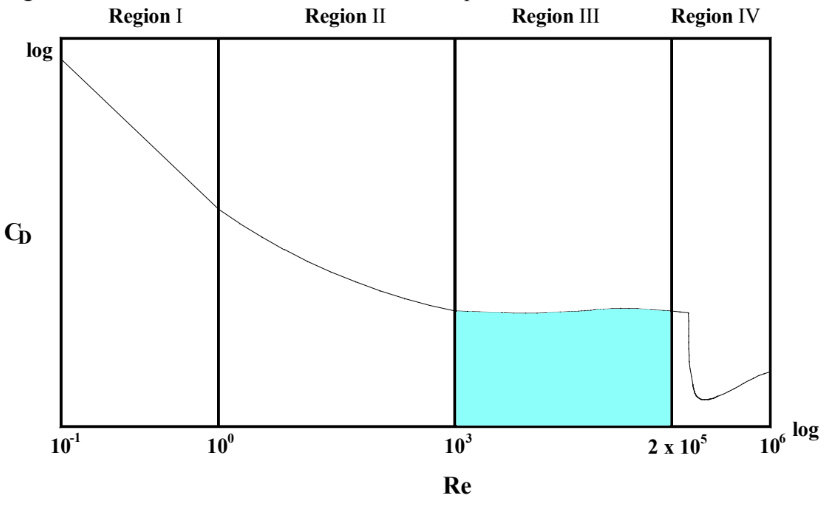
Region 3 Discussion

At Reynold’s number these high, the main component of drag is pressure drag. Viscous drag will always be present in any system where a fluid has some viscosity, but the pressure drag is so dominant here that viscous drag becomes negligible. Viscous effects are mostly seen in the laminar boundary layer surrounding the object. A figure representing the flow figure can be found here:

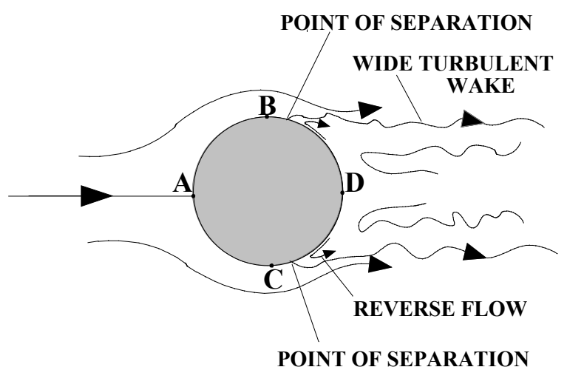
Since the object is moving faster than in other regions, the pressure at A is much higher (more compression of fluid particles). The points of minimum pressure are at B and C. The pressure gradient from A to B and C causes for the particles to accelerate, so as the pressure falls, a thin laminar boundary layer forms.

After points B and C, the boundary particles surrounding the object begin to decelerate, accumulating and thus regaining pressure. Fluid particles will still be flowing (relatively) from B and C to point D against a pressure gradient. This is what causes for the particles on the boundary to separate. When the particles separate, they begin to flow with the pressure gradient. Behind the sphere (point D), the pressure is higher than at B and C, so fluid particles in this region begin to flow back to B and C from point D. Remember though, we still have fluid particles flowing from point A to points B and C. So the fluid in front of the sphere is flowing forward while the fluid’s flow behind the sphere is reversed. The combination of these two effects are what create the eddy currents and the wake region behind the sphere.

How wide is the turbulent wake though? This depends on how fast the fluid particles behind the object are able to decelerate and regain their pressure. If this happens rapidly, fluid particles flowing after B and C are “stalled” quickly, and can accumulate close to the points B and C.

In this region (1000 < Re < 20,000), the coefficient of drag is simply a constant, approximately equal to 0.44.