Drag – Region 1 Discussion
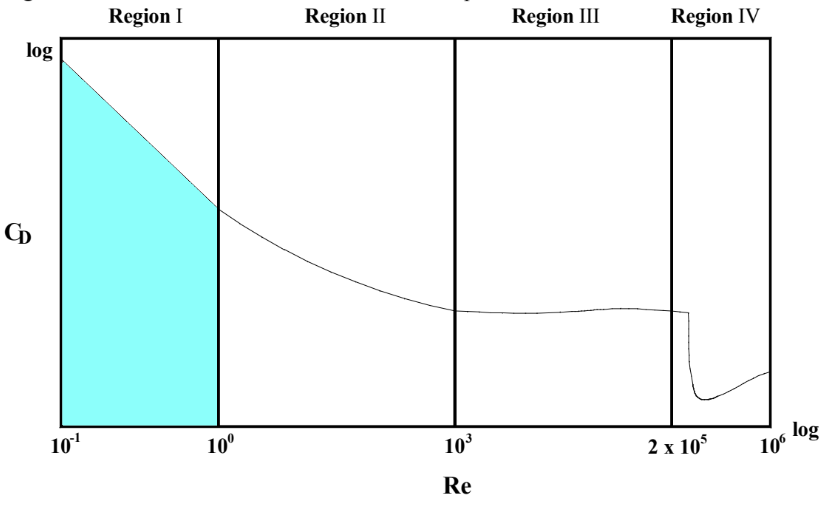
Objects in this region are moving at relatively slow velocities. This is characterized by the low Reynold’s number (smaller velocity leads to lower Reynold’s number). A streamline diagram is shown below:
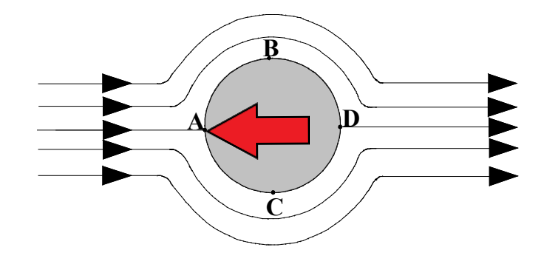
The red arrow indicates the direction of movement of the object while the black arrows indicate the relative velocity of the stream lines of fluid
Here, the main type of drag is basically only viscous drag, with a negligible amount contributing by pressure drag. This is consistent with our understanding of pressure drag. Since the relative velocity between the object and fluid is low, the fluid particles in front of the object isn’t compressed to a degree where there is significant uneven distribution of pressure. We understand that then the only the viscous properties of the fluid can affect the drag. This is further characterized by the straight line of this region. Discussions of eddy currents and points of separation can be found in regions 3 and 4.
The pressure at A is higher than B and C, and the pressures at B and C are higher than at D; however, the pressure gradient across these 4 points are low enough that the fluid particles on the surface of the object do not separate (the fluid momentum is low). Since the fluid passing along the surface is slowing down, and the pressure gradient is decreasing, the boundary layer on the fluid does not separate. Again, I know this sounds confusing now but keep this in mind when reading about the other regions. Combining this idea with the more complicated regions (2, 3 and 4) will help you wrap your head around these concepts.
Now lets look at the mathematics here. Stokes found the following relationship exists in this region (laminar regions):
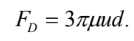
Therefore, from our original Cd equation, we can show that:

This equations shows why this region is characterized by a decreasing straight line (Cd decreases with an increasing Re proportionally).